前言
KMP也是困扰我许久的算法了,道理感觉能懂,但是一到代码就难以理解
但是所幸我现在终于是搞懂了
记一些笔记,希望帮到未来的自己和更多学习的人
前置概念
主串
也叫匹配串、模式串,相当于是要进行搜索的范围
子串
主串中包含的连续的字符
模板串
需要搜索的目标,如果能够在主串中找到与自身相同的子串即为匹配成功
朴素匹配算法
也叫幼稚匹配、简单匹配算法,就是暴力
KMP思路

比如我们要在如图所示的主串中找到该模板串,
请先不要以计算机的思维去想如何实现,我们先以人类的思维入手——
我们总是会先找以g开头的部分,而不是一个一个去比对:

如图,我们大概能在进行第三次匹配时成功
总结一下就是:
顺序遍历主串,不回溯
移动模板串并跳过不必要的回溯
(这里的移动实际上就是遍历,移动只是一个利于结合图文进一步理解的说法——毕竟一个字符串能怎么动,还能在内存里面运动起来不成?)
next数组
既然要跳过不必要的回溯,那么该往哪里跳就成了我们要考虑的问题,先来看下面这个例子
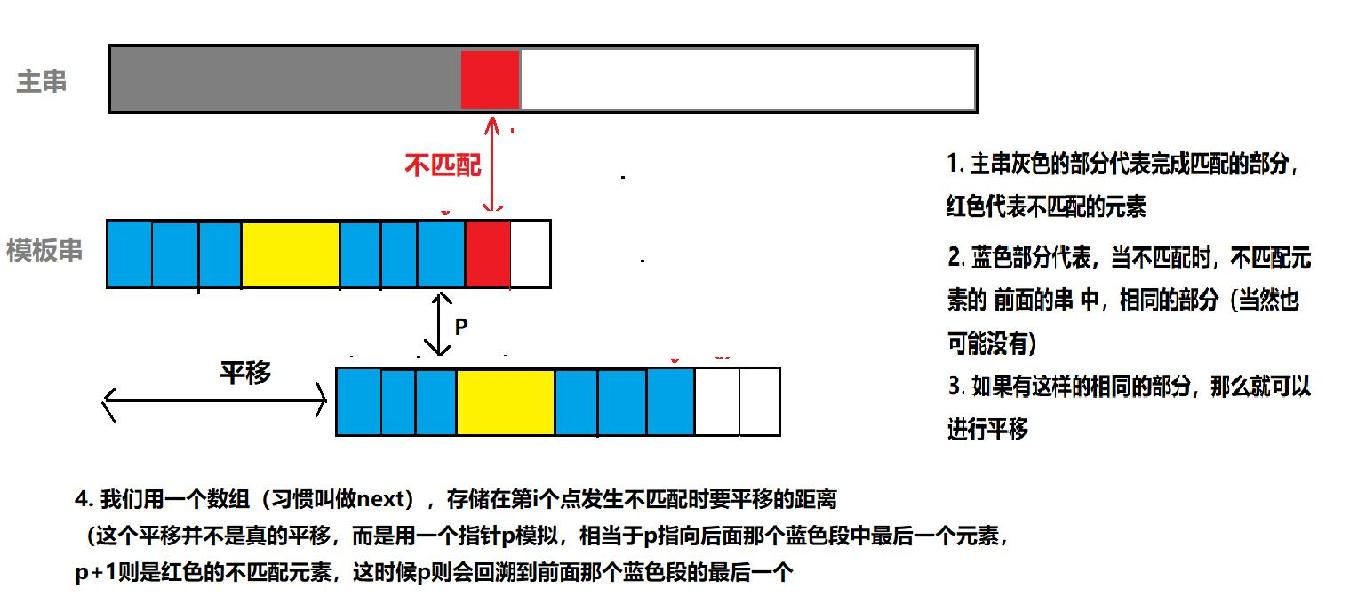
next数组是要记录“平移的距离”,其实也就是记录出现不匹配时,p指针应该回溯到的位置
那么该如何去求这个数组呢?
其实就是要记录(结合图片把下面这句话好好捋一捋)
出现不匹配的元素前面的 字符串中的 相同的最长的 前缀 和 后缀
如果理解了这句话,那么也不难发现求next数组只需要观察模板串
举个例子
这里我们习惯是下标从1开始,这样会有很多好处——我们后面再提
而且此处next[i]代表,当第i+1个元素不匹配时指针p应该回溯的位置——所以下标为0是有意义的
| 元素 | a | b | c | a | b |
|---|---|---|---|---|---|
| 下标 i | 1 | 2 | 3 | 4 | 5 |
| next[i] | 0 | 0 | 0 | 1 | 2 |
手动求取的过程如下:
注意前缀和后缀是串的真子集
| 下标i | 讨论的串 | 最长相同前后缀 | 结果 |
|---|---|---|---|
| 1 | a | 不讨论 | i=1时,若回溯,则一定是到0 |
| 2 | ab | 无 | 不匹配则只能重新开始,回溯到0 |
| 3 | abc | 无 | 同上 |
| 4 | abca | a | 回溯到第一个a,也就是i = 1这里 |
| 5 | abcab | ab | 回溯到第第一个b,也就是i = 2这里 |
其实对于i=5的情况来说已经不用讨论了,因为到了这一步已经是完全匹配上了,但是我们还是把它记录下来
代码实现
const int N = 1e5 + 10;
int next[N];
char t[N]; // 模板串
// 数组下标均从1开始,但根据上文可知next[1]是默认为0的不用求,所以i从2开始
// 而且从2开始相较于从1开始会省去不少麻烦
// 而j从0开始是为了一种试探性的比较
for (int i = 2, j = 0; i <= n; i ++)
{
// j + 1是试探性地比较,不匹配则递归回溯直到 匹配或者j为0
while (j && t[i] != t[j + 1])
{
j = next[j];
}
// 跳出while的原因有两种,如果是因为匹配而跳出
// 那么就让试探性的j + 1真正地进一步
if(t[i] == t[j + 1])
{
j ++;
}
// 可以自己推导一下,在经历上述步骤后,
// j已经代表了此时讨论的串中最长相同前后缀的长度
next[i] = j;
}开始匹配
在求完next数组后
就要开始进行匹配了,匹配的思路 和 求next异曲同工
// i是主串的下标,j+1是模板串下标,j仍可以用来试探next数组
for (int i = 1, j = 0; i <= m; i ++) {
// S是主串,P是模板串
while (j && S[i] != P[j + 1]) {
j = next[j];
}
if (S[i] == P[j + 1]) {
j ++;
}
if (j == n) {
cout << i - n << " ";
// 我们如果要找出主串中所有的模板串,那么就进行下一步,回溯
j = next[j];
}
}完整代码
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
const int M = 1e6 + 10;
int n, m;
char P[N], S[M];
int ne[N];
int main() {
cin >> n >> P + 1 >> m >> S + 1;
for (int i = 2, j = 0; i <= n; i ++) {
while (j && P[i] != P[j + 1]) {
j = next[j];
}
if (P[i] == P[j + 1]) {
j ++;
}
next[i] = j;
}
for (int i = 1, j = 0; i <= m; i ++) {
while (j && S[i] != P[j + 1]) {
j = next[j];
}
if (S[i] == P[j + 1]) {
j ++;
}
if (j == n) {
cout << i - n << " ";
j = next[j];
}
}
return 0;
}


